使用 Python 在 Excel 中进行可视化数据分析：使用箱线图

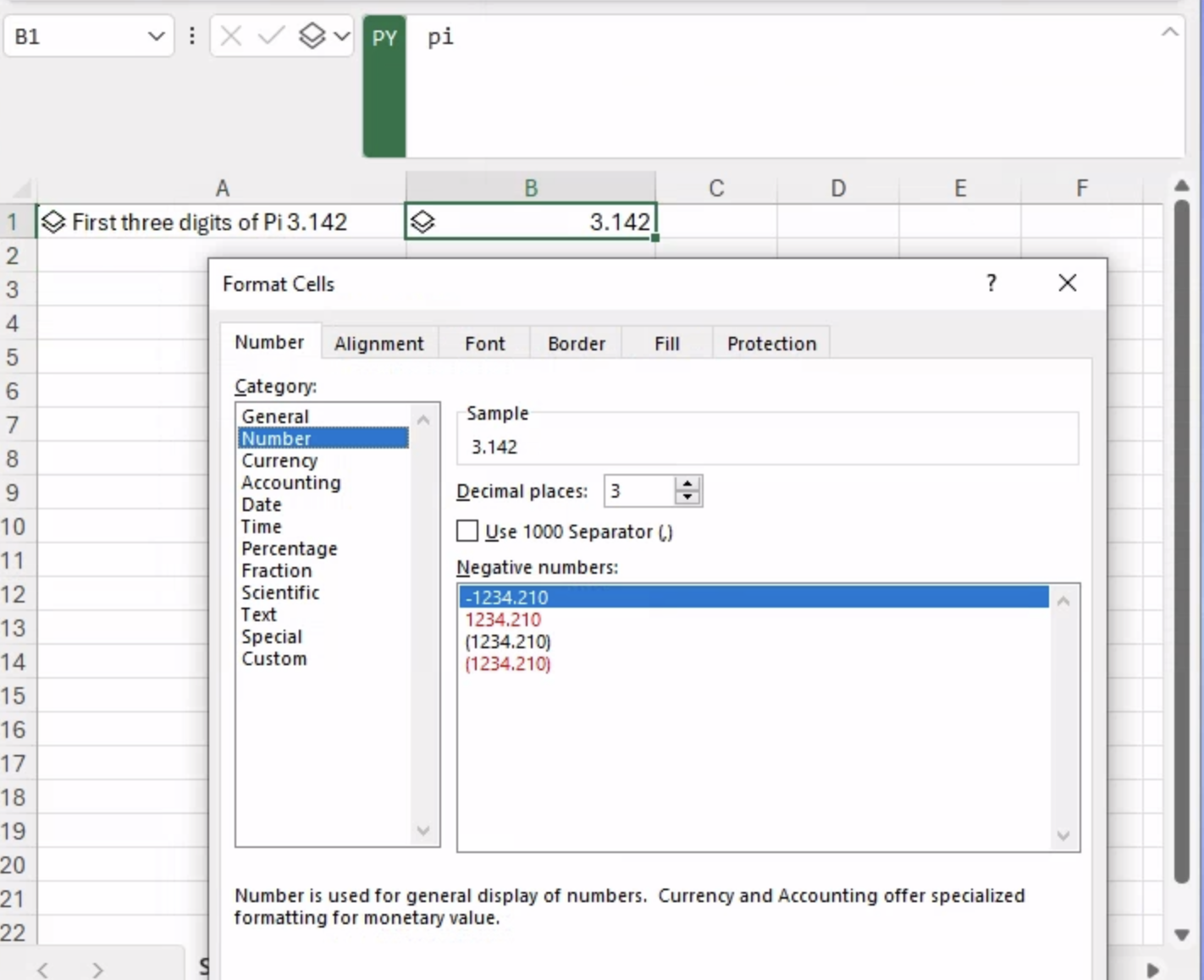
这是教你使用 Microsoft Excel 中的 Python 代码以可视化方式分析数据的博客文章系列中的第二篇。

如果您不熟悉 Python 在 Excel 中的使用，您应该从我的 Python for Excel Analysts 博客系列开始，该系列涵盖了本博客系列中会假设的许多概念。

本系列将使用 Microsoft Excel Labs Python 编辑器 来编写代码。但是，Python 编辑器不是必需的。所有代码都可以使用公式栏和新的 PY() 函数 输入。

本系列中的每篇文章都附带一个 Microsoft Excel 工作簿供您下载使用，以培养您的技能。本篇文章的工作簿可供 下载。

为了方便起见，以下是本系列中所有博客文章的链接

• 第 1 部分 - 使用直方图
• 第 2 部分 - 使用箱线图（本篇文章）
• 第 3 部分 - 使用散点图
• 第 4 部分 - 使用条形图
• 第 5 部分 - 使用折线图

注意：要重现本篇文章中的示例，安装Python 在 Excel 中的试用版。如果您喜欢本博客系列，请查看我的自定进度的认证计划，Anaconda 认证：使用 Python 在 Excel 中进行数据分析。

了解使用四分位数的分布

如本博客系列的第 1 部分所述，通过可视化检查原始数据来从一列数字中得出见解，随着列的增大，很快就会变得不可能。

第 1 部分演示了直方图如何直观地表示一列数字中的数字是如何分布的。使用直方图可以从包含数千个值的列中得出见解。以下是一个示例直方图，在第 1 部分中进行了讨论

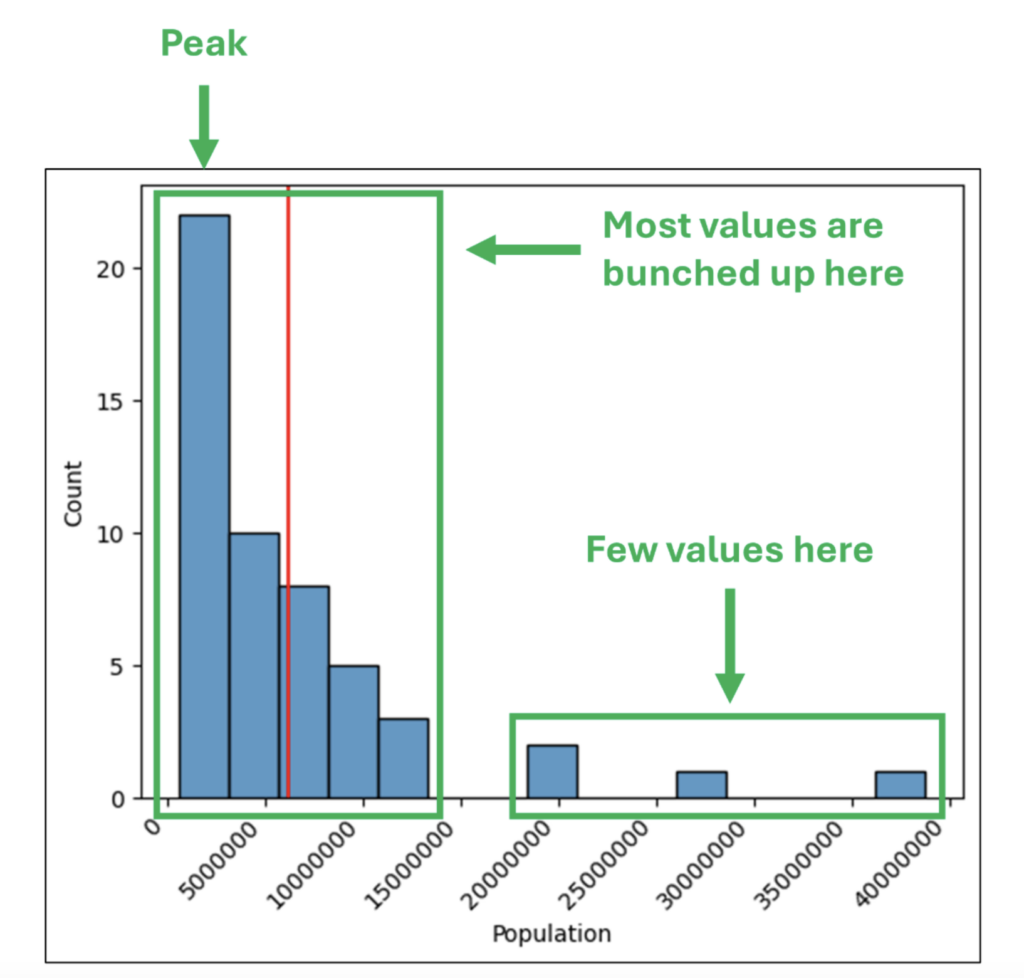
图 01 - 本博客系列第 1 部分中的直方图

虽然直方图非常有用，但它们并不是唯一可以用来从数字列中得出见解的数据可视化方法。

箱线图 是另一种可视化数字列分布的方法。箱线图与直方图的不同之处在于它们使用四分位数来描述分布。

中位数

理解四分位数的最简单方法是考虑中位数。中位数定义为代表一列数字的第 50 个百分位的数值。换句话说，中位数是第 2 个四分位数。

从概念上讲，中位数代表给定一组数字（例如，数据帧中的数字列）的典型值。

考虑以下 10 个数字。这些数字是从本篇文章 Excel 工作簿中的 ResellerSales 表中提取的

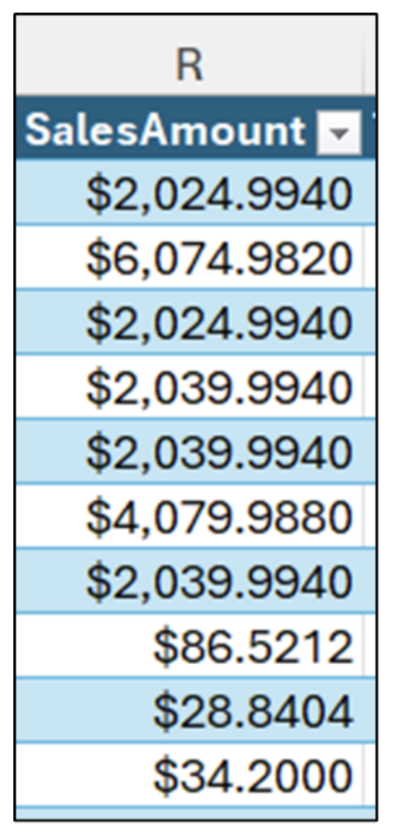
图 02 - 从 ResellerSales 表中提取的十个数字

通过可视化检查数据，可以合理地推测这些 10 个数字的典型值为约 2,000 美元。这些 10 个数字的平均值（或均值）为 2,047 美元，证实了这一推测。

现在考虑一下：如果将最后一个值替换掉，这 10 个数字现在变为如下所示

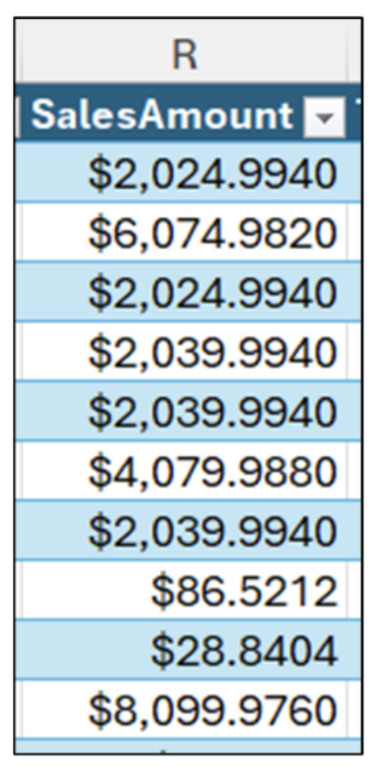
图 03 - 一组新的 10 个数字

通过可视化检查图 03 中显示的数据，可以得出以下结论

• 一半的值约为 2,000 美元。
• 两个值低于 2,000 美元。
• 三个值高于 2,000 美元。

可以认为，这 10 个数字的典型值的合理推测仍然是 2,000 美元。

但是，这 10 个值的平均值现在是 2,854 美元，比 2,000 美元更接近 3,000 美元！

我们可以将典型值的合理推测和平均值与使用中位数进行比较。

找到中位数的第一步是对图 03 中的数据进行排序

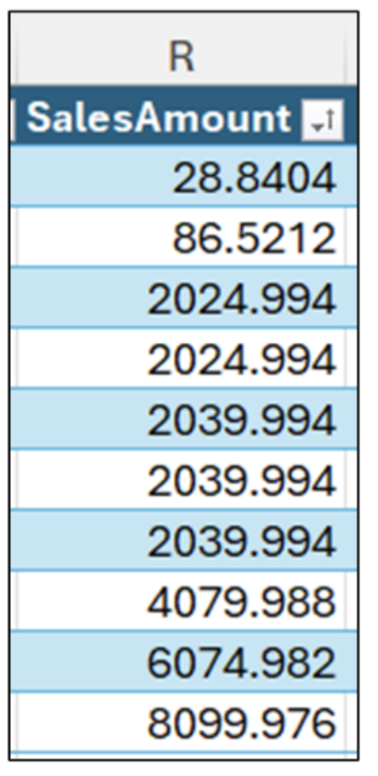
图 04 - 排序后的数据

接下来，中位数是排序后的数据中间的值

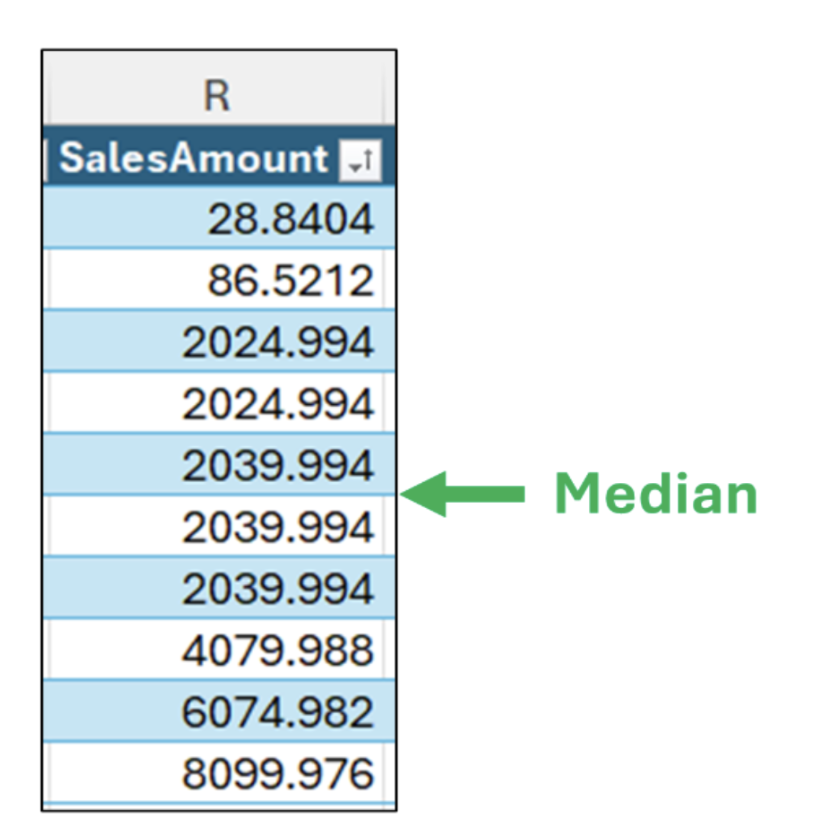
图 05 - 数据的中位数

如图 05 所示，当您有偶数个数字值（例如，本例中的 10 个）时，没有一个单一的中位数值。

在这种情况下，中位数的计算方法是排序后数据中间两个值的平均值。在本例中，这两个值相同，因此中位数为 2,039.994 美元。

此示例说明了为什么中位数作为数字列的典型值很有用。

与平均值相比，较小/较大的值对中位数的影响较小。

从中位数到四分位数

如上所述，中位数代表一组数字数据的第 50% 值，或第 2 个四分位数，并代表数据集合的典型值。

还可以使用额外的四分位数来帮助描述分布的范围。

例如，通过在图 05 中添加第 1 个和第 3 个四分位数，我们可以开始看到数据中的值是如何分布的

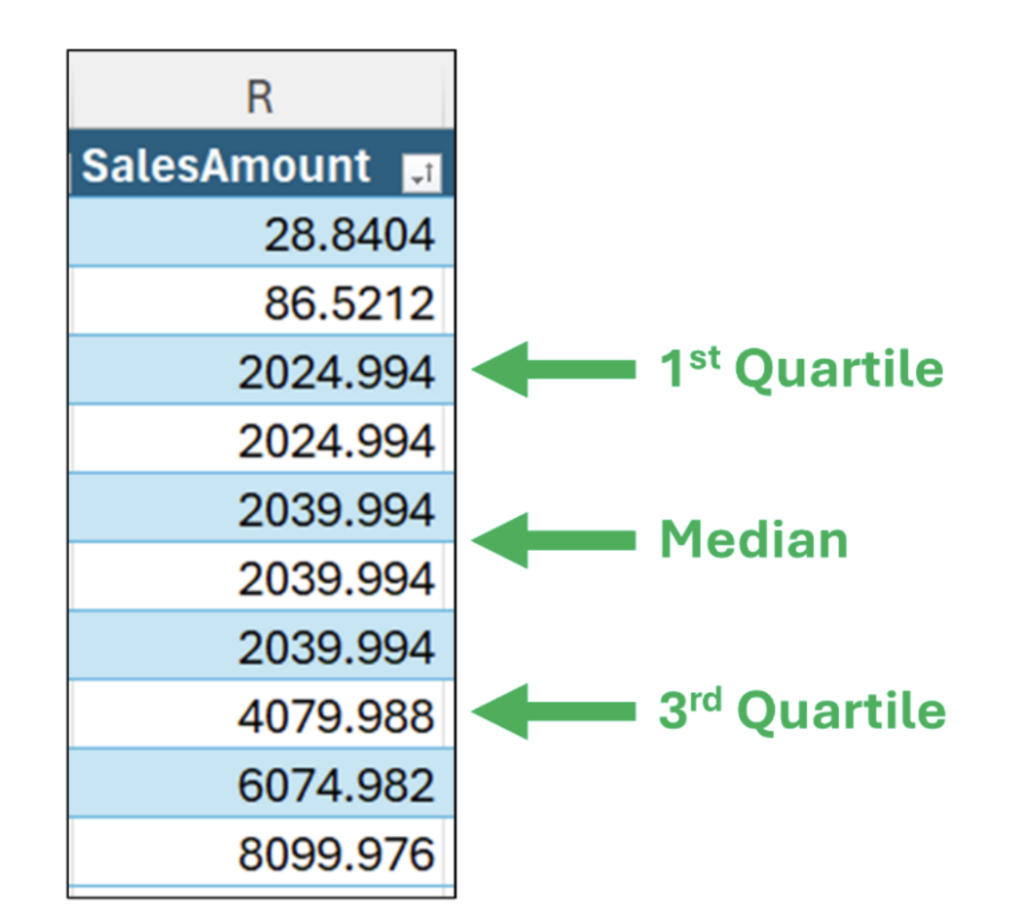
图 06 - 添加第 1 个和第 3 个四分位数

注意：图 06 是第 1 个和第 3 个四分位数的概念表示。精确的计算方式略有不同。

当然，图 06 并没有很好地演示使用四分位数来描述数字数据的分布的价值。

使用箱线图来描述大量数值的分布时，使用四分位数的强大之处就会变得很明显。

您的第一个箱线图

箱线图与直方图一样，是一种非常强大的可视化数字数据列分布的方法。箱线图利用四分位数来说明数字数据的分布。

箱线图的强大之处在于它们可以根据类别来可视化分布。

本篇文章将使用本篇文章 Excel 工作簿中包含的 ResellerSales 表中的数据。

ResellerSales 表包含基于 Microsoft 的 AdventureWorks 数据仓库 示例数据库的假设销售数据。

数据包含 60,855 行和 23 列数据。对于本篇文章，将使用以下三列：SalesTerritoryGroup、SalesAmount 和 OrderDate。

编写箱线图代码

在本篇文章中，我们将使用箱线图来分析 ResellerSales 表的 SalesAmount 列的分布。

箱线图通常使用来自 Excel 表的两个列构建 - 一列数字和一列类别。

首先，以下 Python 代码使用 pandas 库 加载 ResellerSales Excel 表

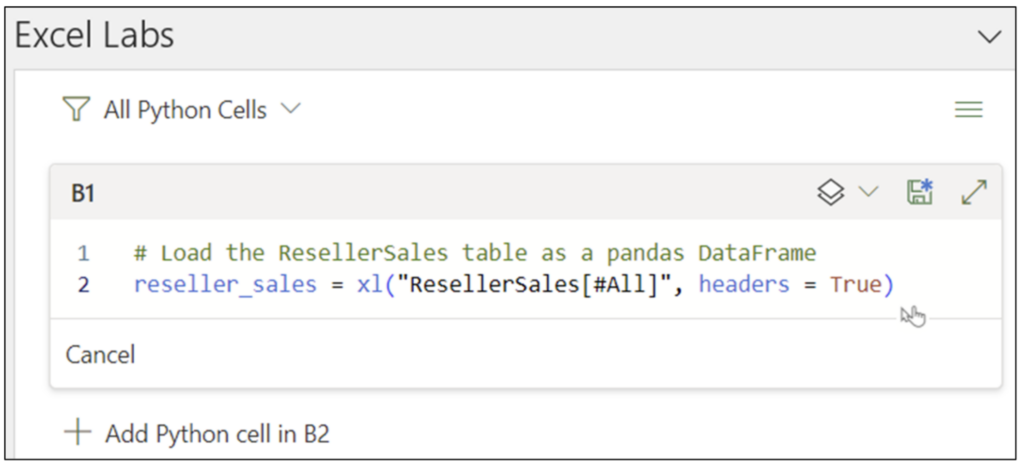
图 07 - 用于加载 ResellerSales Excel 表的 Python 代码

注意：虽然上面的 Python 代码是使用 Excel Labs Python 编辑器编写的，但这并不是必需的。

单击 Python 编辑器中的磁盘图标执行 Python 代码

图 08 - Python 代码执行

将数据加载为数据帧后，以下 Python 代码使用 seaborn 库 使用 SalesAmount 和 SalesTerritoryGroup 列创建箱线图

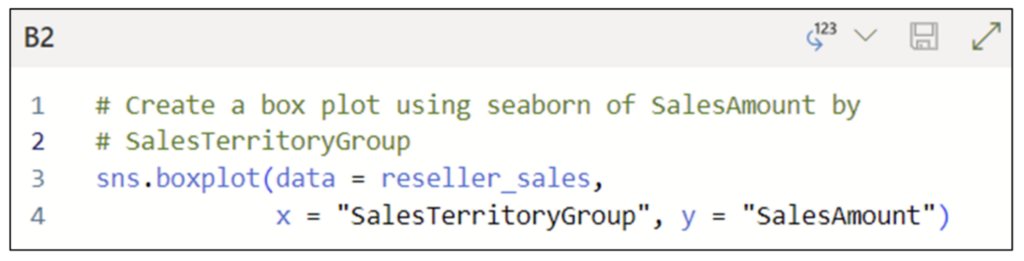
图 09 - 用于创建箱线图的 Python 代码

单击 Python 编辑器中单元格的向下箭头，可以选中“转换为 Excel 值”选项。使用此选项会在工作表单元格内呈现箱线图

图 10 - 在工作表单元格内呈现箱线图

执行箱线图代码会呈现可视化

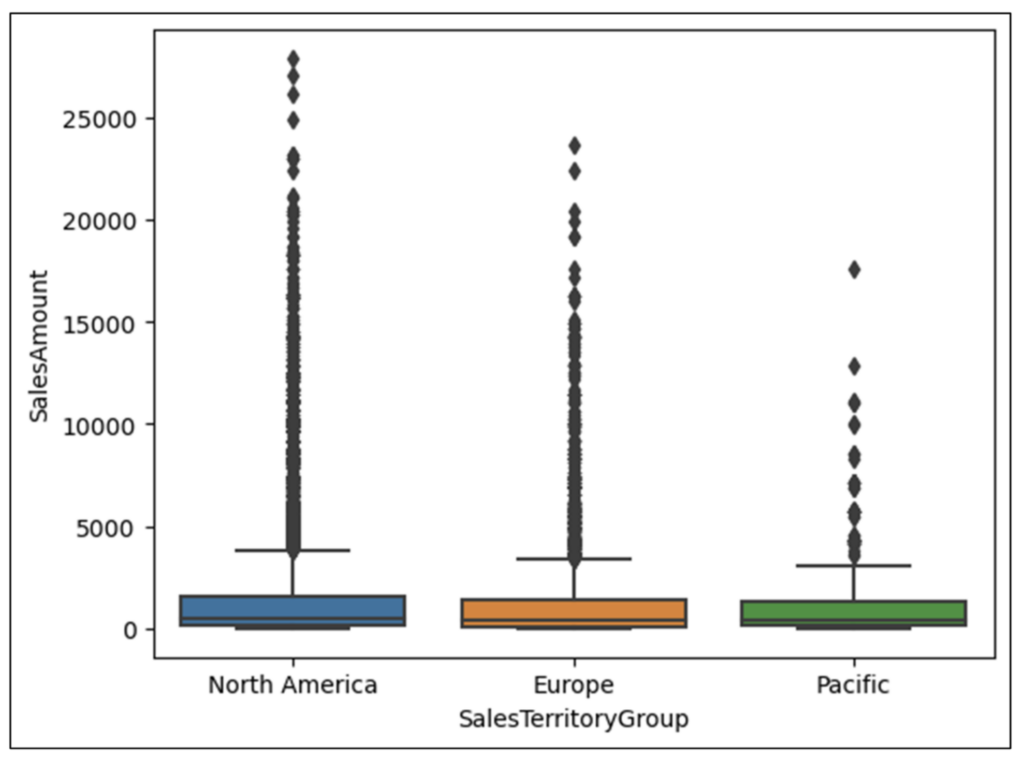
图 11 - 按 SalesTerritoryGroup 分组的 SalesAmount 箱线图

箱线图提供了对 SalesAmounts 的强大见解。但是，要获得这些见解，您必须知道如何解读箱线图。

解读箱线图

以下 Python 代码筛选 reseller_sales 数据帧并将其可视化为箱线图。筛选可以简化可视化效果

图 12 - 筛选 reseller_sales 数据帧并将其可视化为箱线图

注意：图 12 显示了配置为“转换为 Excel 值”选项的代码单元格。

执行上述代码会生成以下箱线图

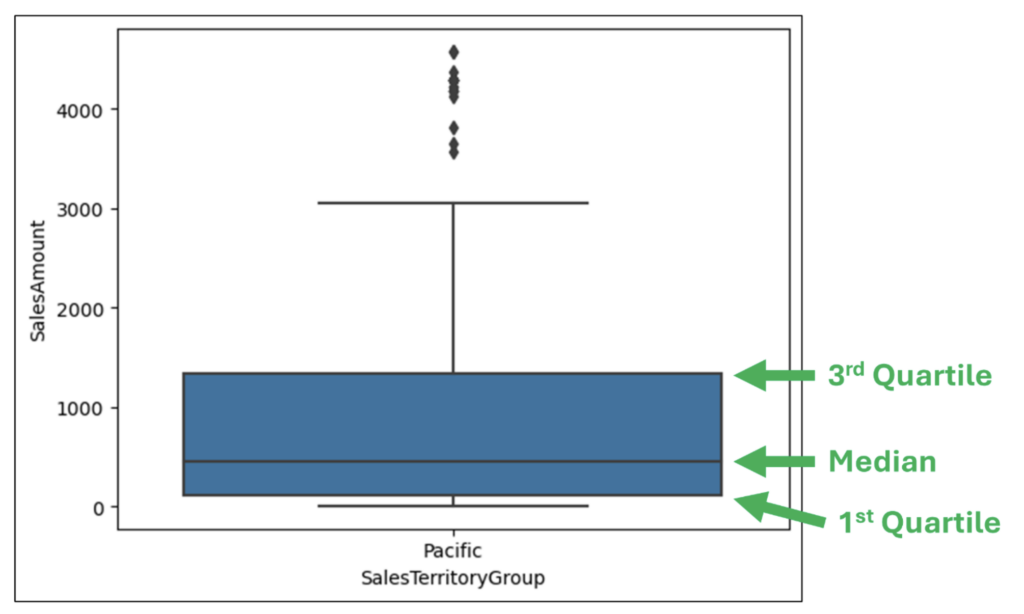
图 13 - 按 SalesTerritoryGroup 分组的 SalesAmount 筛选后的箱线图

图 13 说明了如何解读箱线图中的箱体

• 箱体的顶部表示数据的第 75 个百分位数（即，75% 的值小于这条线）。
• 箱体的底部表示数据的第 25 个百分位数（即，25% 的值小于这条线）。
• 箱体顶部和底部之间的线是数据的中位数（即，第 50 个百分位数）。

通过检查箱体，我们可以获得有关太平洋销售区域组销售额分布的许多见解（图 13）。

• 箱体的顶部显示，75% 的销售额远低于 2000 美元。
• 中位线显示，50% 的销售额约为 500 美元或更少。
• 鉴于中位线位于箱体下三分之一的位置，销售额偏向较低的值。

从分析的角度来看，以上情况引发了以下需要深入数据挖掘的问题。

• 哪些产品与销售额偏向较低的值有关？
• 哪些客户与销售额偏向较低的值有关？
• 是否有其他因素（例如折扣）导致销售额偏向较低的值？

使用箱线图分析数值数据的下一个方面是考虑“须”。

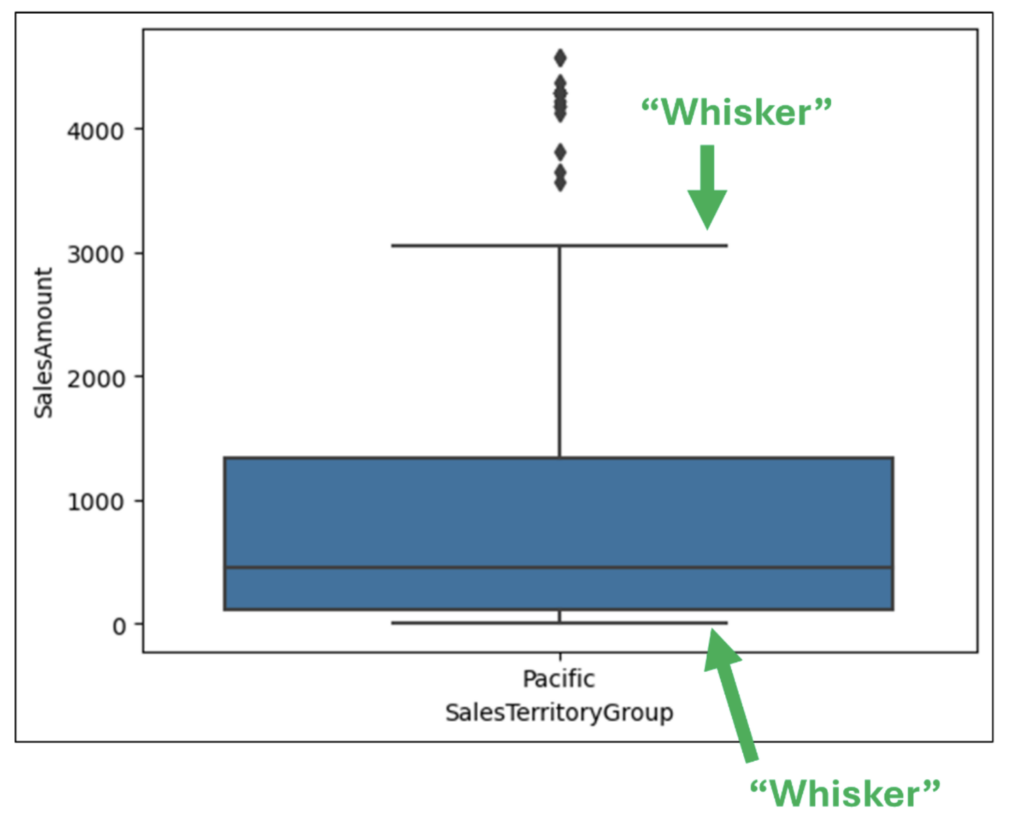
图 14 – 箱线图“须”

箱线图中的须以可视方式显示大于第 75 个百分位数和小于第 25 个百分位数的值的分布。

直观地说，须越长，数据中的值分布越分散。反之，须越短，数据中的值分布越集中。

检查图 14 可以得出以下示例见解。

• 上须比下须长得多，表明销售额范围约为 1200 美元到 3000 美元。
• 下须非常短，表明大多数较低的销售额范围为 0 美元到约 100 美元。

从分析的角度来看，检查这些须会引发以下额外问题。

• 过去的销售额是否高于现在？
• 随着时间的推移，是否引入了新的低成本产品，从而可能导致销售额出现偏差？
• 随着时间的推移，促销折扣的使用是否发生了变化？

使用箱线图分析数值数据的最后一个方面是考虑“离群值”。

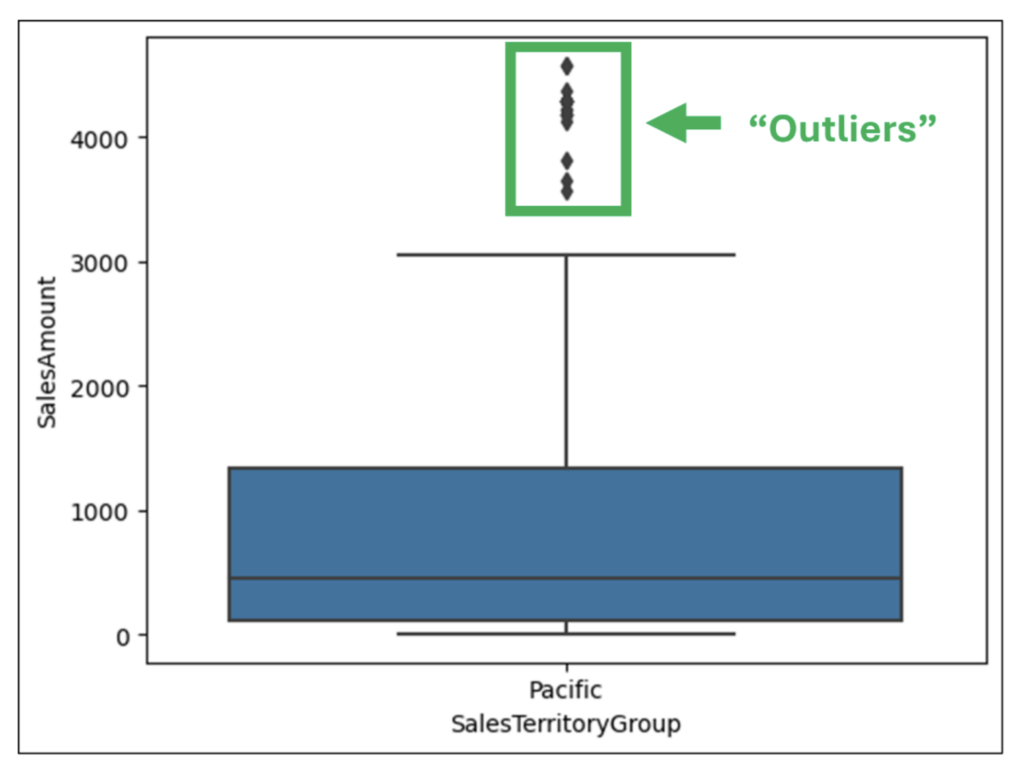
图 15 – 箱线图“离群值”

箱线图使用标准化计算来确定须的长度（有关详细信息，请参见下文）。位于须之外的任何值都被称为“离群值”。

检查图 15 可以获得有关销售额离群值的见解。

• 存在许多离群的较大销售额。
• 不存在离群的较小销售额。

需要进一步分析这些离群值，以了解与这些值相关的模式数据。例如，

• 离群的销售额是否源自少数大型客户？
• 离群的销售额是否一直保持一致？

虽然许多上述分析问题也可以通过检查直方图来生成，但正如我们将在本文档的后面部分看到的那样，箱线图提供了超出离群值的更多分析功能。

离群值的数学

虽然确定箱线图中须的长度有很多方法，但以下介绍了最常用的计算方法。

用于构建箱线图须的第一个计算是四分位距 (IQR)。在箱线图中，IQR 是第 3 个四分位数和第 1 个四分位数之间的差值（即箱体的高度）。

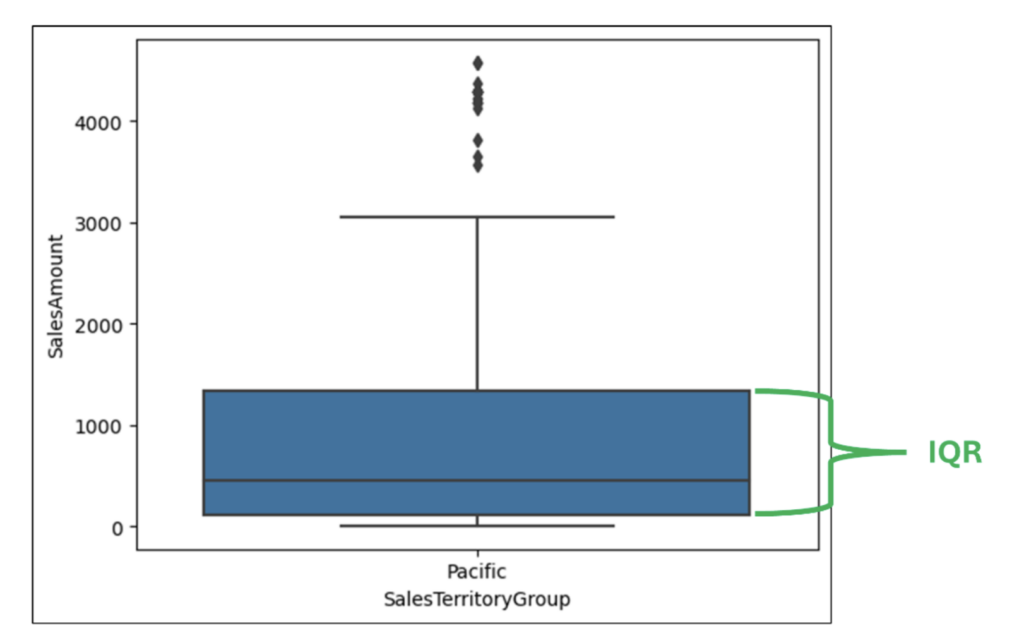
图 16 – 四分位距 (IQR)

要计算上须，使用以下逻辑。

• 最大数据值或…
• 第 75 个百分位数 + (1.5 * IQR)…
• 以较小者为准。

要计算下须，使用以下逻辑。

• 最小数据值或…
• 第 25 个百分位数 – (1.5 * IQR)…
• 以较大者为准。

随时间推移的箱线图

使用箱线图分析数据时，通常会生成与时间相关的分析问题。例如，销售额值的分布是否随着时间的推移而发生变化？

这是箱线图相对于直方图的一个优势所在 - 你可以将时间（例如年份）视为一个类别！

以下代码将一个订单年份列添加到经销商销售数据框中，然后使用新列按订单年份创建销售额的箱线图。

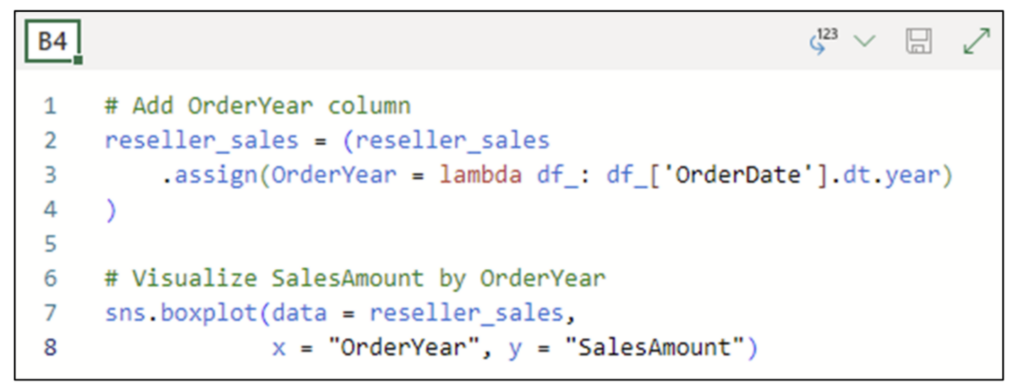
图 17 – 使用箱线图可视化销售额按订单年份

注意：图 17 显示了配置为转换为 Excel 值选项的代码单元格。

执行图 17 中显示的代码会在工作表单元格内呈现箱线图。

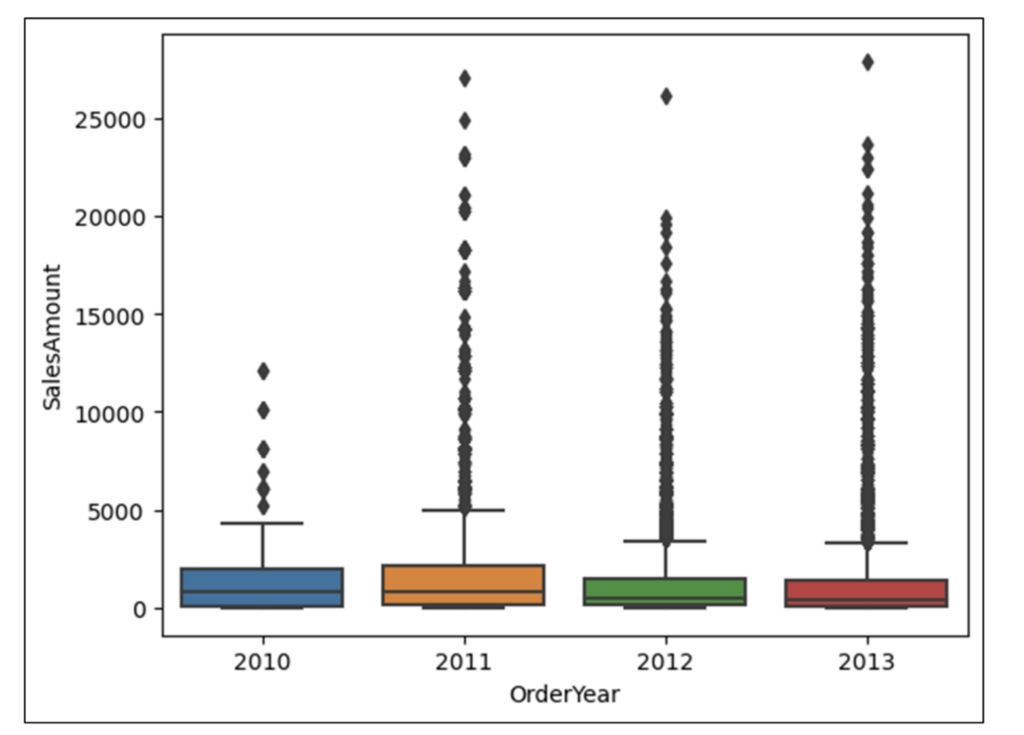
图 18 –销售额按订单年份的箱线图

检查图 18 中描绘的箱线图，可以获得一些有趣的见解。

• 2012/2013 年箱体的高度低于 2010/2011 年箱体的高度。这表明销售额的分布在后期年份偏向更小的值。
• 2012/2013 年的上须比相应的 2010/2011 年上须短。这进一步表明销售额在后期年份偏向更小的值。
• 后期年份似乎有更多离群的较大销售额值。

图 18 中描绘的箱线图确认需要进行更多分析（例如，上面列出的问题）才能了解更多信息。

下一步是什么？

本文档介绍了如何使用箱线图分析数值数据，包括将类别和时间纳入分析。

本系列的下一篇文章将继续使用此分析场景，通过探索使用散点图的两个数字列之间的关系来进行探索。

下次再见，祝你数据侦查愉快！